Provable Security Basics

Three steps:

• Precisely specify threat model

  • formal model and definition of what security means

• Propose a construction

• Write a formal proof

  • Show that under the threat mode if assumption X holds,then the construction is secure.

Textbook RSA

why Textbook RSA is insecure?

about RSA padding

与对称加密算法DES，AES一样，RSA算法也是一个块加密算法（ block cipher algorithm），总是在一个固定长度的块上进行操作，即需要填充消息，但跟AES等不同的是，block length是跟key length有关的。

举例：想传输的密文为No, ASCII 为 0x4E 0x6F， 所以得到明文 M = 0x4E6F

密文 C = Pow (0x4E6F, 3) mod n , 计算 Pow (0x4E6F, 3) = 0x75CCE07084F， 也就是 C = 0x75CCE07084F mod n
我们知道n是一个4096位的大数，肯定大于0x75CCE07084F

所以我们可以直接得到密文 C = 0x75CCE07084F
破解：敌军将0x75CCE07084F 转成10进制，得到8095174953039
再尝试着进行开根操作，开到3次根的时候$\sqrt[3]{8095174953039}$ = 20079
接着转十六进制 hex(20079)= 0x4E4F
遂破密

安全性不足的原因在于：密文进行指数e运算时，得到的值小于n的值，导致加密过程与n关系不大，没有模数缩减

解决方案：默认e为65537，扩大指数e，保证值必定大于n

但这样同样带来相同明文无论加密多少次，都得到相同密文的问题

解决方案：补位算法

填充方式	待填充长度	填充后长度
RSA_NO_PADDING	不填充	和公钥等长
RSA_PKCS1_PADDING	至少RSA_size(rsa) - 11	和公钥等长
RSA_PKCS1_OAEP_PADDING	RSA_size(rsa) - 41	和公钥等长

RSA_NO_PADDING填充模式，如果明文不够128字节，加密的时候会在明文前面填充若干数据0，直至达到128字节。

RSA_PKCS1_PADDING填充模式，如果明文不够128字节，加密的时候会在明文中随机填充一些数据，所以会导致对同样的明文每次加密后的结果都不一样。

EB = 00 || BT || PS || 00 || D ，其中D为the message

BT（The block type块类型）：
BT=00 or 01 （私钥运算时）
BT=02 （公钥运算时）

PS（The padding string填充字符串）：
BT=00，PS由00组成；
BT=01，PS由FF组成；
BT=02，PS由伪随机生成，且非零；

PS长度为Len(EB) - 3 - Len(D)，最少是8字节

RSA_PKCS1_OAEP_PADDING填充模式，编码方式不同。

When Textbook RSA is Used to Protect the Privacy of Hundreds of Millions of Users

离线攻击：Meet-in-the-middle attack 中间相遇攻击->同理于为何使用三重DES而不使用两重DES。本质上这类攻击方式为使用空间换取时间。

• 密钥长度不够
• 没有使用安全的填充方式（使用OAEP）
• 加密算法过于简单

单向函数（One-way function）

一个函数 $f: \{0,1\}^n \mapsto \{0,1\}^m$ 被认为是单向的，如果满足以下两个条件：

1. 多项式时间可计算：对于所有的 $x$，函数 $f(x)$ 可以在多项式时间内被计算出来。这意味着给定一个输入 $x$，可以在合理的时间内（与输入长度的多项式相关）计算出输出 $f(x)$。

2. 难以逆转：对于所有概率多项式时间（PPT）算法 $\mathcal{A}$，逆转函数 $f$ 是困难的。也就是说，给定 $f(x)$，找到任何一个 $x'$ 使得 $f(x') = f(x)$ 的概率非常小，不超过某个小的误差值 $\varepsilon(n)$。这里的 $\varepsilon(n)$ 是一个随着输入长度 $n$ 变化的函数，表示逆转函数的难度。

单向函数 $\text{Invert}_{\mathcal{A}, f}(n)$

步骤如下：

1. 随机选择输入：随机选择一个输入 $x$ 从集合 $\{0,1\}^n$ 中。

2. 计算函数输出：对于每个 PPT 算法 $\mathcal{A}$，计算 $y = f(x)$。

3. 逆转尝试：算法 $\mathcal{A}$ 尝试找到一个 $x'$，使得 $f(x') = y$。逆转实验的成功概率定义为在随机选择 $x$ 的情况下，算法 $\mathcal{A}$ 能够找到正确的 $x'$ 的概率。

4. 验证结果：如果算法 $\mathcal{A}$ 找到了一个 $x'$ 使得 $f(x') = y$，则实验返回 1，否则返回 0。

$f(x)$为一个单向函数，$f(m)$和$f(m||r)$都不是关于m的承诺方案，因为commitment需要保证hiding和binding，可能该输出会泄露m中的部分比特信息，但如果$f$是一个random oracle，那么$f(m||r)$是一个承诺。

---

离散对数问题（Discrete Logarithm Problem）

群生成算法：$g$ 是一个通用的、多项式时间的群生成算法。

• 当输入为 $1^n$（这里 $n$ 通常表示安全参数，如比特数）时，算法 $g$ 输出一个循环群 $G$ 的描述，
• 群的阶（即群中元素的数量）为 $q$（满足 $|q|=n$），以及一个生成元 $g \in G$。

离散对数问题的难度：我们说相对于算法 $g$，离散对数问题是难解的，如果对于所有概率多项式时间（PPT）算法 $\mathcal{A}$，其优势函数 $\operatorname{Adv}_{\mathcal{A},\mathcal{G}}^{DLog}(n)$ 满足以下条件：

$\operatorname{Adv}_{\mathcal{A},\mathcal{G}}^{DLog}(n) := \left|\operatorname{Pr}\left[DLog_{\mathcal{A},\mathcal{G}}(n)=1\right]-\frac{1}{q}\right| \leq \varepsilon(n)$

这里，$\operatorname{Pr}[DLog_{\mathcal{A},\mathcal{G}}(n)=1]$ 表示算法 $\mathcal{A}$ 成功解决离散对数问题的概率，$q$ 是群的阶，$\varepsilon(n)$ 是一个随着安全参数 $n$ 变化的函数，表示允许的安全误差范围。

离散对数 $DLog_{\mathcal{A},\mathcal{G}}(n)$

步骤如下：

1. 生成群和生成元：运行群生成算法 $\mathcal{G}(1^n)$，生成群 $G$、阶 $q$ 和生成元 $g$。Generate(G,q,g)$\leftarrow$$\mathcal{G}$($1^n$)
2. 选择一个随机元素：从群 $G$ 中均匀随机选择一个元素 $h$。Choose a uniform h $\leftarrow$G
3. 算法 $\mathcal{A}$ 的尝试：算法 $\mathcal{A}$ 尝试找到满足 $g^x = h$ 的 $x$，其中输入为群 $G$、阶 $q$、生成元 $g$ 和元素 $h$。Obtain x $\leftarrow$A(G,q,g,h)
4. 验证结果：如果算法 $\mathcal{A}$ 找到了正确的 $x$，即 $g^x = h$，则实验返回 1，否则返回 0。Return $1\;if\;g^x = h$

这个定义说明，如果不存在有效的多项式时间算法能够解决离散对数问题，那么这个问题就被认为是难解的。离散对数问题的难解性是许多公钥密码系统和数字签名算法安全性的基础，例如 Diffie-Hellman 密钥交换和 ElGamal 加密系统。

基于DH的密钥协商协议（DHKE）

DHKE.Setup($1^n$)

• 生成群和生成元：算法接收一个安全参数 $1^n$（通常表示为比特数），并使用群生成算法 $\mathcal{G}$ 生成一个循环群 $G$、群的阶 $q$ 和群的生成元 $g$。
• 返回全局密钥：算法返回全局密钥 $gk := (G, q, g)$，这些信息将被用于后续的密钥生成过程。

DHKE.Keygen(gk)

• 随机选择私钥：对于给定的全局密钥 $gk$，算法随机选择一个私钥 $s$ 从整数环 $Z_q$ 中。
• 计算公钥：算法计算公钥 $h := g^s$，其中 $g$ 是生成元，$s$ 是随机选择的私钥。
• 返回密钥对：算法返回私钥 $sk := s$ 和公钥 $pk := h$。

DHKE.SK(gk, sk, pk)

• 计算共享密钥：给定全局密钥 $gk$，一方的私钥 $sk$ 和另一方的公钥 $pk$，算法计算共享密钥 $k := pk \cdot sk$。在这个上下文中，$pk \cdot sk$ 表示将私钥 $s$ 与公钥 $h$（即 $g^s$）相乘，得到共享密钥。

下一步尝试证明DHKE安全性。

关于Diffie-Hellman密钥交换（DHKE）协议在某种假设（X assumption）下的安全性问题。

1. 形式化NIKE的安全性：

2. 确定X

3. 通过归约提供证明

• 确定假设和安全性->what is secure? DHCK在哪些假设下是安全。

  • 敌手：第三方
  • 敌手能力：只能看
  • 攻击目标：得到$k=g^{st}$

• 使用规约来证明 DHCK可以在多项式时间内被归约到特定假设 -> 若假设是困难的，则说明被证明的密码方案很难攻破，则说明具有安全性。

关于密钥恢复（Key Recovery）算法的安全性的安全定义和安全模型 (这块有什么用呢?)

密钥恢复安全性(NIKE)

NIKE协议由三个算法组成：Setup（设置）、Keygen（密钥生成）、SK（密钥推导）。

密钥恢复安全性的定义：我们说一个NIKE协议是密钥恢复安全的，如果对于所有概率多项式时间（PPT）算法 $\mathcal{A}$，其优势函数 $\operatorname{Adv}_{\mathcal{A}, KE}^{KR}(n)$ 满足以下条件：

$\operatorname{Adv}_{\mathcal{A}, KE}^{KR}(n) := \left|\operatorname{Pr}\left[KR_{\mathcal{A}, KE}(n)=1\right]-\frac{1}{|\mathcal{K}|}\right| \leq \varepsilon(n)$

这里，$\operatorname{Pr}[KR_{\mathcal{A}, KE}(n)=1]$ 表示算法 $\mathcal{A}$ 成功恢复密钥的概率，$|\mathcal{K}|$ 是可能的密钥总数，$\varepsilon(n)$ 是一个随着安全参数 $n$ 变化的函数，表示允许的安全误差范围。

密钥恢复实验 $KR_{\mathcal{A}, KE}(n)$

实验步骤如下：

1. 生成全局参数：运行 Setup 算法，生成全局密钥 $gk$。Generate gk<-Setup(n)
2. 生成第一对密钥：使用 Keygen 算法和全局密钥 $gk$ 生成第一对密钥 $(sk_1, pk_1)$。Run ($sk_1$,$pk_1$) $\leftarrow$ Keygen(gk)
3. 生成第二对密钥：同样使用 Keygen 算法和全局密钥 $gk$ 生成第二对密钥 $(sk_2, pk_2)$。Run ($sk_2$$pk_2$) $\leftarrow$ Keygen(gk)
4. 密钥恢复尝试：算法 $\mathcal{A}$ 尝试从全局密钥 $gk$ 和两个公钥 $pk_1, pk_2$ 中恢复出密钥，得到 $k'$。Obtain $k'\leftarrow A(gk,pk_1,pk_2)$
5. 验证恢复结果：如果 $k'$ 等于使用 SK 算法从全局密钥 $gk$、私钥 $sk_1$ 和公钥 $pk_2$ 推导出的密钥，则实验返回 1，否则返回 0。Return $1 \;if\;k' = SK(gk,sk_1,pk_2)$

如果能够证明即使在攻击者拥有公钥和全局参数的情况下，也无法在多项式时间内有效地恢复出私钥。那么就可以认为DHKE协议是密钥恢复安全的。

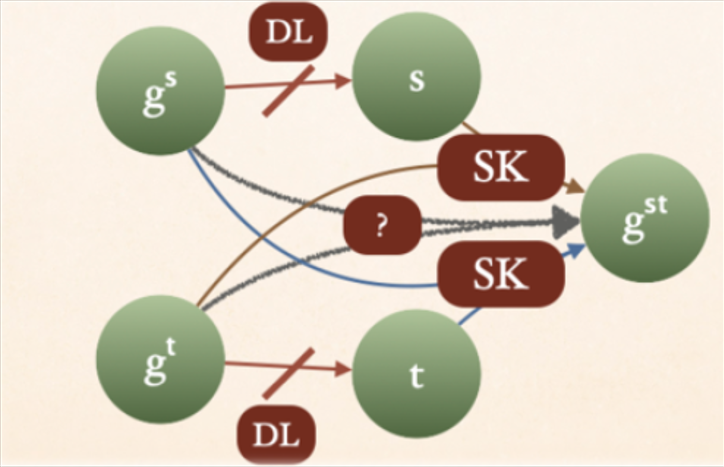
目标

证明Diffie-Hellman密钥交换（DHKE）协议是密钥恢复（KR）安全的。意味着即使攻击者拥有公钥和全局参数，也无法在多项式时间内有效地恢复出私钥。尝试通过归约到离散对数（DL）假设来证明DHKE的密钥恢复安全性。离散对数假设是密码学中的一个基本假设，它表明在特定的群中，给定一个生成元和一个元素，计算它们之间的离散对数是困难的。

符号

• DL：代表离散对数假设。
• SK：可能代表密钥推导算法或秘密密钥。
• st：可能代表某种状态或设置。
• g：通常在Diffie-Hellman协议中代表生成元。

---

计算性Diffie-Hellman（CDH）假设

定义：我们说相对于群生成算法 $g$，CDH问题是难解的，如果对于所有概率多项式时间（PPT）算法 $\mathcal{A}$，其优势函数 $\operatorname{Adv}_{\mathcal{A},\mathcal{G}}^{CDH}(n)$ 满足以下条件：

$\operatorname{Adv}_{\mathcal{A},\mathcal{G}}^{CDH}(n) := \left|\operatorname{Pr}\left[CDH_{\mathcal{A},\mathcal{G}}(n)=1\right]-\frac{1}{q}\right| \leq \varepsilon(n)$

这里，$\operatorname{Pr}[CDH_{\mathcal{A},\mathcal{G}}(n)=1]$ 表示算法 $\mathcal{A}$ 成功解决CDH问题的概率，$q$ 是群的阶，$\varepsilon(n)$ 是一个随着安全参数 $n$ 变化的函数，表示允许的安全误差范围。

计算性Diffie-Hellman $CDH_{\mathcal{A},\mathcal{G}}(n)$

实验步骤如下：

1. 生成群和生成元：运行群生成算法 $\mathcal{G}(1^n)$，生成群 $G$、阶 $q$ 和生成元 $g$。
2. 随机选择私钥：随机选择两个私钥 $s$ 和 $t$ 从整数环 $Z_q$ 中。
3. 算法 $\mathcal{A}$ 的尝试：算法 $\mathcal{A}$ 尝试找到 $g^{st}$，其中输入为群 $G$、阶 $q$、生成元 $g$、$g^s$ 和 $g^t$。
4. 验证结果：如果算法 $\mathcal{A}$ 找到了正确的 $u$ 使得 $u = g^{st}$，则实验返回 1，否则返回 0。

CDH假设是基于Diffie-Hellman密钥交换的一个问题，它假设即使给定了 $g^s$ 和 $g^t$，计算 $g^{st}$ 也是困难的。这个假设是许多密码学协议，包括一些加密算法和数字签名算法的安全性基础。

因此若CHD是困难的，那么说明DL也是困难的，同时若DL是困难的，那么CDH问题在某些条件下才是困难的

---

通过归约证明如果计算性Diffie-Hellman（CDH）问题是难解的，那么离散对数（DLog）问题也是难解的。

定理：如果相对于群生成算法 $\mathcal{G}$，CDH问题是难解的，那么相对于同一算法 $\mathcal{G}$，离散对数问题也是难解的。

离散对数 $DLog_{\mathcal{A},\mathcal{G}}(n)$

具体实验步骤同上处$DLog_{\mathcal{A},\mathcal{G}}(n)$

不可区分安全(IND Security)

每次使用一个新的随机密钥k，对m进行异或操作，给定密文c和随机值，敌手很难在多项式时间内判断哪个是随机值，哪个是密文。

敌手在多项式时间内无法确定特定数据，哪个是随机选取的，哪个是正确生成的

IND安全性

IND安全性的定义：我们说一个NIKE协议KE是IND安全的，如果对于所有概率多项式时间（PPT）算法 $\mathcal{A}$，其优势函数 $\operatorname{Adv}_{\mathcal{A}, KE}^{IND}(n)$ 满足以下条件：

$\operatorname{Adv}_{\mathcal{A}, KE}^{IND}(n) := \left|\operatorname{Pr}\left[\operatorname{IND}_{\mathcal{A}, KE}(n)=1\right]-\frac{1}{2}\right| \leq \varepsilon(n)$

这里，$\operatorname{Pr}[\operatorname{IND}_{\mathcal{A}, KE}(n)=1]$ 表示算法 $\mathcal{A}$ 能够区分两个密钥中的一个的概率，$\frac{1}{2}$ 是随机猜测的概率，$\varepsilon(n)$ 是一个随着安全参数 $n$ 变化的函数，表示允许的安全误差范围。

IND安全性实验 $\operatorname{IND}_{\mathcal{A}, KE}(n)$

实验步骤如下：

1. 生成全局参数：运行 Setup 算法，生成全局密钥 $gk$。
2. 生成第一对密钥：使用 Keygen 算法和全局密钥 $gk$ 生成第一对密钥 $(sk_1, pk_1)$。
3. 生成第二对密钥：同样使用 Keygen 算法和全局密钥 $gk$ 生成第二对密钥 $(sk_2, pk_2)$。
4. 计算一个共享密钥：使用 SK 算法和全局密钥 $gk$、私钥 $sk_1$ 和公钥 $pk_2$ 计算共享密钥 $k_0$。
5. 随机选择另一个密钥：从密钥空间 $\mathcal{K}$ 中均匀随机选择另一个密钥 $k_1$。
6. 随机选择一个密钥：随机选择一个比特 $b \in \{0,1\}$。
7. 攻击者尝试区分：算法 $\mathcal{A}$ 尝试区分哪个是真实的共享密钥，输入为全局密钥 $gk$、公钥 $pk_1$、$pk_2$ 和密钥 $k_b$。
8. 验证结果：如果算法 $\mathcal{A}$ 正确猜测了 $b$，则实验返回 1，否则返回 0。

在计算性Diffie-Hellman（CDH）假设下，Diffie-Hellman密钥交换（DHKE）协议是IND安全的？

Answer: 如果DHKE协议在CDH假设下是IND安全的，这意味着即使攻击者拥有公钥和全局参数，也无法在多项式时间内区分两个密钥中的一个，除非他们能够解决CDH问题。这通常意味着协议能够抵抗被动攻击，即攻击者只能监听通信但不能主动干预。要证明这一点，通常需要展示如果存在一个能够区分密钥的攻击者，那么可以利用这个攻击者来解决CDH问题，从而表明如果CDH问题是难解的，那么DHKE协议就是IND安全的。

决策性Diffie-Hellman（DDH）假设

定义：我们说相对于群生成算法 $g$，DDH问题是难解的，如果对于所有概率多项式时间（PPT）算法 $\mathcal{A}$，其优势函数 $\operatorname{Adv}_{\mathcal{A},\mathcal{G}}^{DDH}(n)$ 满足以下条件：

$\operatorname{Adv}_{\mathcal{A},\mathcal{G}}^{DDH}(n) := \left|\operatorname{Pr}\left[DDH_{\mathcal{A},\mathcal{G}}(n)=1\right]-\frac{1}{2}\right| \leq \varepsilon(n)$

这里，$\operatorname{Pr}[DDH_{\mathcal{A},\mathcal{G}}(n)=1]$ 表示算法 $\mathcal{A}$ 能够正确区分给定的三个元素是随机生成的还是由Diffie-Hellman过程生成的概率，$\frac{1}{2}$ 是随机猜测的概率，$\varepsilon(n)$ 是一个随着安全参数 $n$ 变化的函数，表示允许的安全误差范围。

DDH问题实验 $DDH_{\mathcal{A},\mathcal{G}}(n)$

实验步骤如下：

1. 生成群和生成元：运行群生成算法 $\mathcal{G}(1^n)$，生成群 $G$、阶 $q$ 和生成元 $g$。
2. 随机选择私钥：随机选择三个私钥 $x$、$y$ 和 $z$ 从整数环 $Z_q$ 中。
3. 随机选择比特：随机选择一个比特 $b \in \{0,1\}$。
4. 设置挑战元素：根据 $b$ 的值，设置 $Z_0 := g^z$ 和 $Z_1 := g^{x y}$。
5. 算法 $\mathcal{A}$ 的尝试：算法 $\mathcal{A}$ 尝试判断给定的元素 $g^x$、$g^y$ 和 $Z_b$ 是否由Diffie-Hellman过程生成，即判断 $Z_b$ 是否等于 $g^{x y}$。
6. 验证结果：如果算法 $\mathcal{A}$ 正确猜测了 $b$，则实验返回 1，否则返回 0。

Answer: 如果DDH问题是难解的，那么意味着没有有效的多项式时间算法能够区分Diffie-Hellman生成的元素和随机生成的元素。这为基于Diffie-Hellman的协议提供了一定的安全性保证，因为即使攻击者能够观察到公钥的交换，他们也无法确定这些公钥是否用于生成共享密钥。再结合之前提到的CDH假设和IND安全性，DDH假设提供了另一种视角来分析协议的安全性。如果一个协议在DDH假设下是安全的，那么它可能能够抵抗更广泛的攻击类型，包括那些试图确定公钥是否用于生成有效共享密钥的攻击。

（这里的prove下周会学习）

小结

• 设计一个安全方案时，要先自我下好定义，什么是安全？该方案要达到什么样的安全性，在此基础上再去确定假设、进行安全构造，最后再进行证明。
• 在对一个安全方案进行安全性验证时，可以通过规约的方式，将当前的问题归约到已有的困难问题上。