Commitment Scheme

利用承诺方案，当承诺者需要承诺一条消息 $m$ 时，可以将该消息放入信封中，并在稍后打开信封，公开其承诺的信息

承诺方案具备两个性质

隐藏性：承诺方案不会揭示被承诺的消息
绑定性：承诺者无法将被承诺的消息揭示为两个不同的值，也即揭示阶段无法改变被承诺的值

常见承诺方案的基本流程：

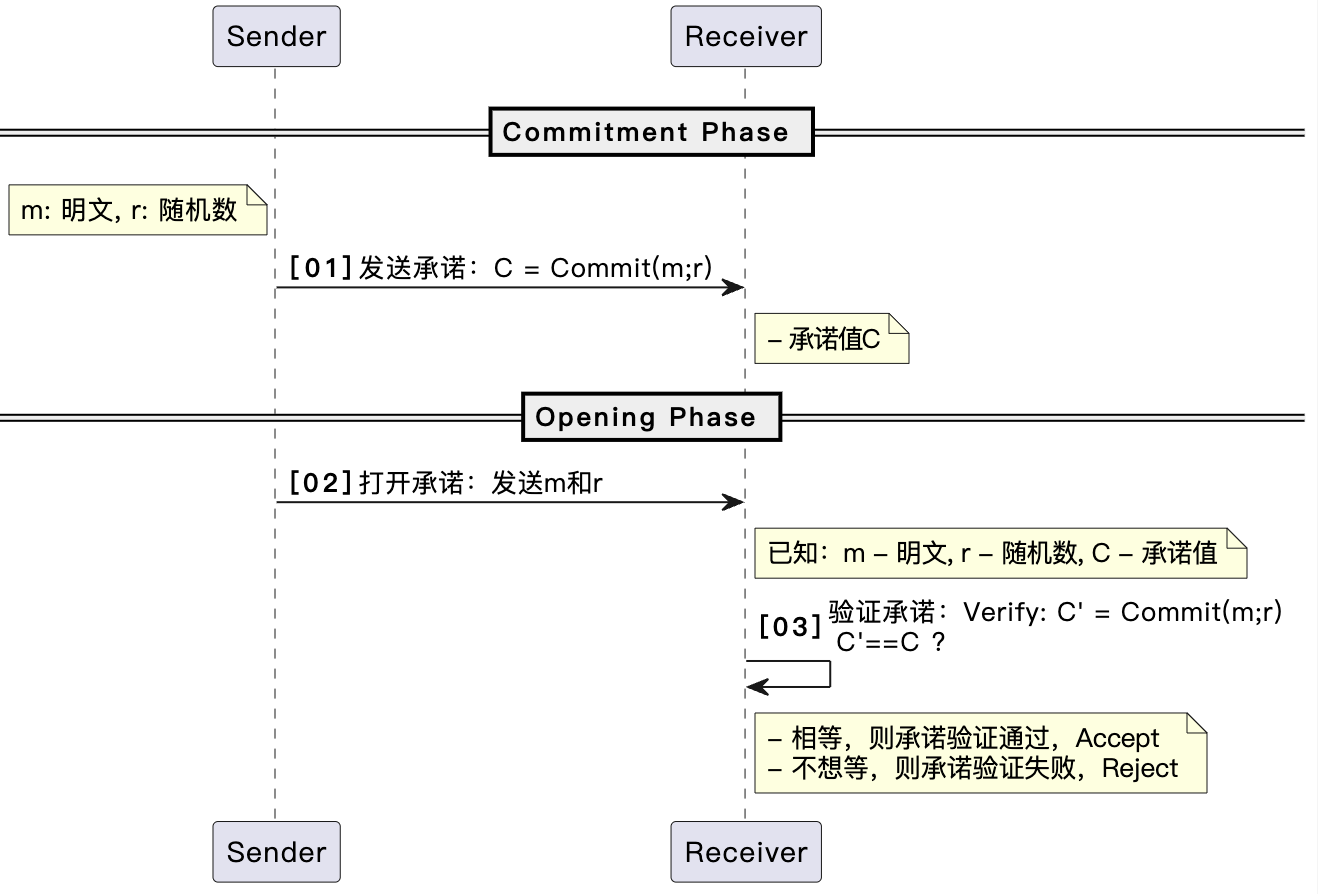
【01】发送承诺：Sender选取随机数r，计算m的承诺值，构造 $C=Commit(m,r)$ ，将承诺值发送给Receiver

【02】打开承诺：发送m与r

【03】验证承诺：Receiver计算 $C'=Commit(m,r)$ ，判断 $C'=C$

哈希承诺

【01】发送承诺：Sender选择一个明文m，计算承诺值 $C=H(m)$ ，将C发送给Receiver

【02】打开承诺：Sender公开明文m

【03】验证承诺：Receiver计算 $C'=H(m)$ ，判断 $C'=C$

缺点：可能会存在哈希碰撞的问题

EIGamal承诺

基于离散对数问题的困难性假设构造的承诺方案。假设 $G_p$ 是阶为 $q$ 的循环群， $g,h$ 是生成元， $m$ 是明文

【01】发送承诺：Sender选择一个明文 $m$ 和一个随机数 $r$ ，计算承诺值 $C=(g^r,m·h^r)$ ，将C发送给Receiver

【02】打开承诺：Sender公开明文m和随机数r

【03】验证承诺：Receiver计算 $C=(g^r,m·h^r)$ ，判断 $C'=C$

建立在发送方难以找到两个不同的 $(r_1,m_1)$ 和 $(r_2,m_2)$ 使得 $C=(g^{r_1},m_1·h^{r_1})=(g^{r_2},m_2·h^{r_2})$

Pedersen承诺

基于离散对数问题的困难性假设构造的承诺方案。假设 $G_p$ 是阶为 $q$ 的乘法群， $g,h$ 是独立生成元， $m$ 是明文

【01】发送承诺：Sender选择一个明文 $m$ 和一个随机数 $r$ ，计算承诺值 $C=g^m·h^r$ ，将 $C$ 发送给Receiver

【02】打开承诺：Sender公开明文m和随机数r

【03】验证承诺：Receiver计算 $C'=g^m·h^r$ ，判断 $C'=C$

接收方无法通过承诺值C推导出明文m，发送方难以找到两个不同的 $(r_1,m_1)$ 和 $(r_2,m_2)$ 满足 $C={g^{m_1}}·{h^{r_1}}={g^{m_2}}·{h^{r_2}}$

原因在于 $g,h$ 是独立生成元，他们生成的子群是没有重叠的，意味着 $g^{m_1-m_2}=h^{r_2-r_1}$ 只能当 $m_1=m_2,r_1=r_2$ 的情况下才成立，故很难找到 $C$ 满足以上式子

基于ECC构造

假设 $G$ 和 $H$ 是椭圆曲线上的点， $m$ 是明文， $r$ 是随机数

【01】发送承诺：Sender选择一个明文 $m$ 和一个随机数 $r$ ，计算承诺值 $C=mG+rH$ ，将 $C$ 发送给Receiver

【02】打开承诺：Sender公开明文m和随机数r

【03】验证承诺：Receiver计算 $C'=mG+rH$ ，判断 $C'=C$

Pedersen承诺的同态性：

两个Pedersen承诺的和=明文之和的Pederson承诺

$C_1={g^{m_1}}·{h^{r_1}}$ 和 $C_2={g^{m_2}}·{h^{r_2}}$ 是两个Pederson承诺， $m_1,m_2$ 是明文， $r_1,r_2$ 是随机数，有

C_1·C_2={g^{m_1}}·{h^{r_1}}·{g^{m_2}}·{h^{r_2}}={g^{m_1+m_2}}·{h^{r_1+r_2}}

commmit(m_1,r_1)·commit(m_2,r_2)=commit(m_1+m_2,r_1+r_2)

基于ECC构造也有此性质

作用：能够保证密态的加法性。即直接验证承诺来检验消息是否为 $m_1+m_2$ 和

零知识证明承诺

允许发送方向接收方证明自己拥有某个明文，而不透露明文的具体内容

交互式零知识证明承诺：发送方和接收方之间需要交互，发送方向接收方发送证明，接收方验证证明
非交互式零知识证明承诺：发送方可以在不与接收方交互的情况下生成证明，接收方可以验证证明

Sigsma交互式零知识证明承诺

基于离散对数问题的困难性假设构造的零知识承诺方案。

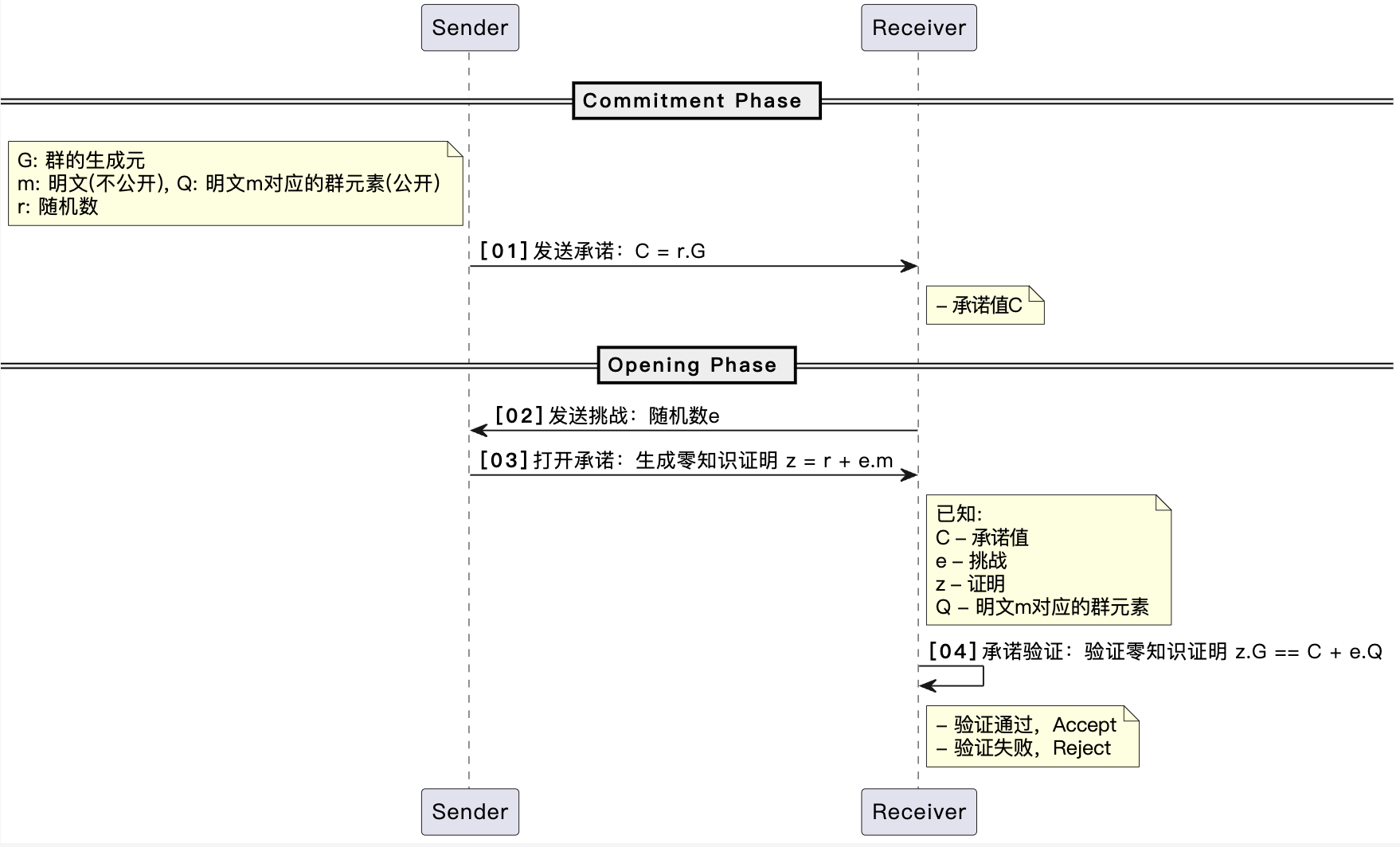
【01】发送承诺：Sender选取随机数 $r$ ，生成承诺 $C=r.G$ ，发送 $C$ 给Receiver

【02】发送挑战：Receiver发送一个随机挑战 $e$ 给Sender

【03】发送挑战：Sender计算证明 $proof:z=m+er$ ，并发送给Receiver

【04】承诺验证：Receiver验证 $Proof$ ，验证 $Z.G==C+e.Q$

正确性：

z.G=(r+e.m).G=r.G+e.m.G=C+e.Q

隐藏性：Receiver只知道C，不知道r的值

绑定性：无法找到多个 $r$ 使得 $C=r_1·G=r_2·G$

零知识性：Receiver只知道 $(Q,C,e,z)$ ，无法计算出 $m$

Sigma非交互式零知识证明承诺

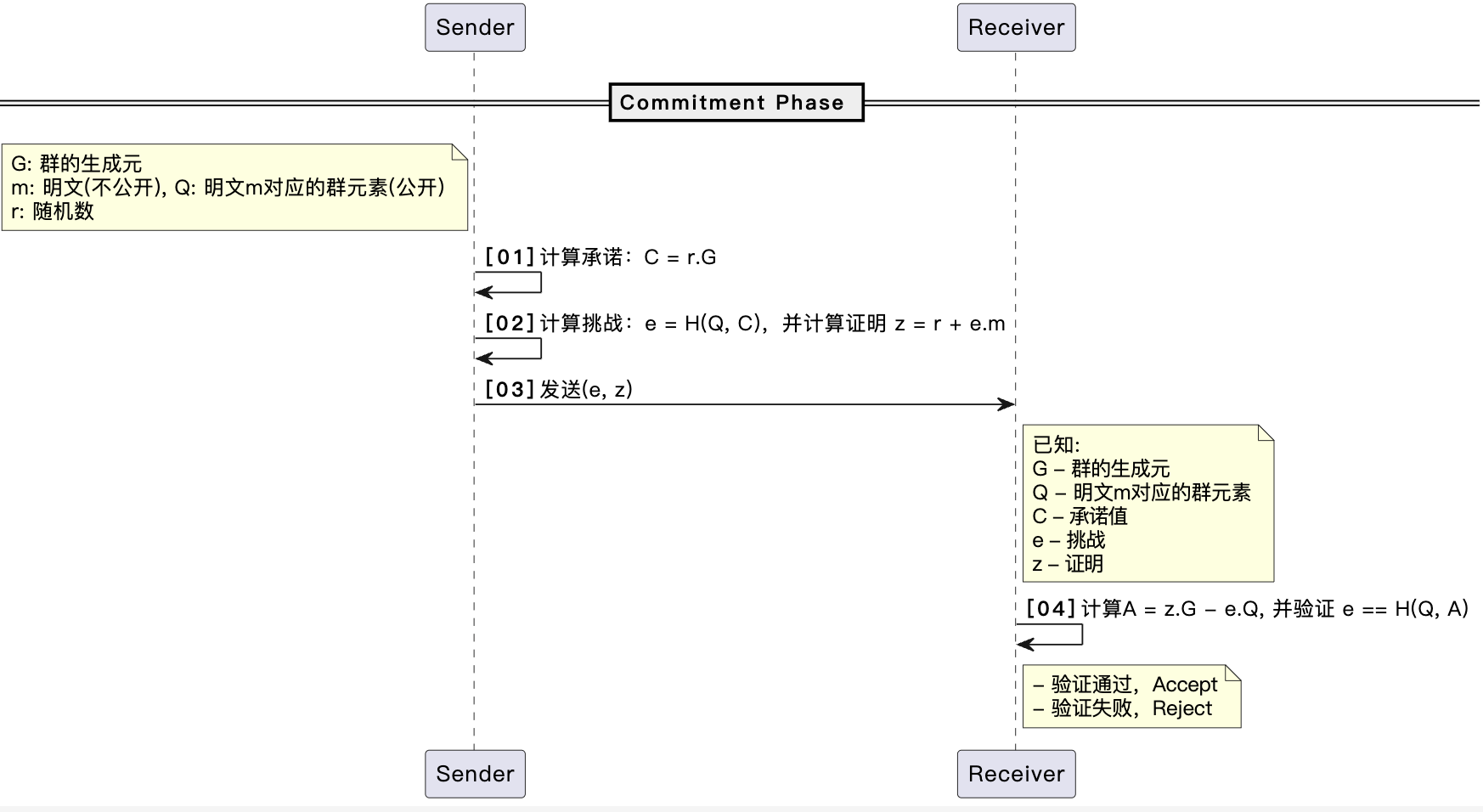
【01】发送承诺：Sender选取随机数 $r$ ，生成承诺 $C=r·G$

【02】生成挑战：Sender计算挑战 $e=H(Q,C)$ ，并计算证明 $z=r+e·m$

【03】发送 $(e,z)$ ：Sender发送给挑战 $e$ 和证明 $z$ 给Receiver

【04】承诺验证：Receiver计算 $A=z·G-e·Q$ ，并验证 $e==H(Q,A)$

特点：无需交互，性能更好，发送数据量更小

Pedersen非交互式零知识证明承诺

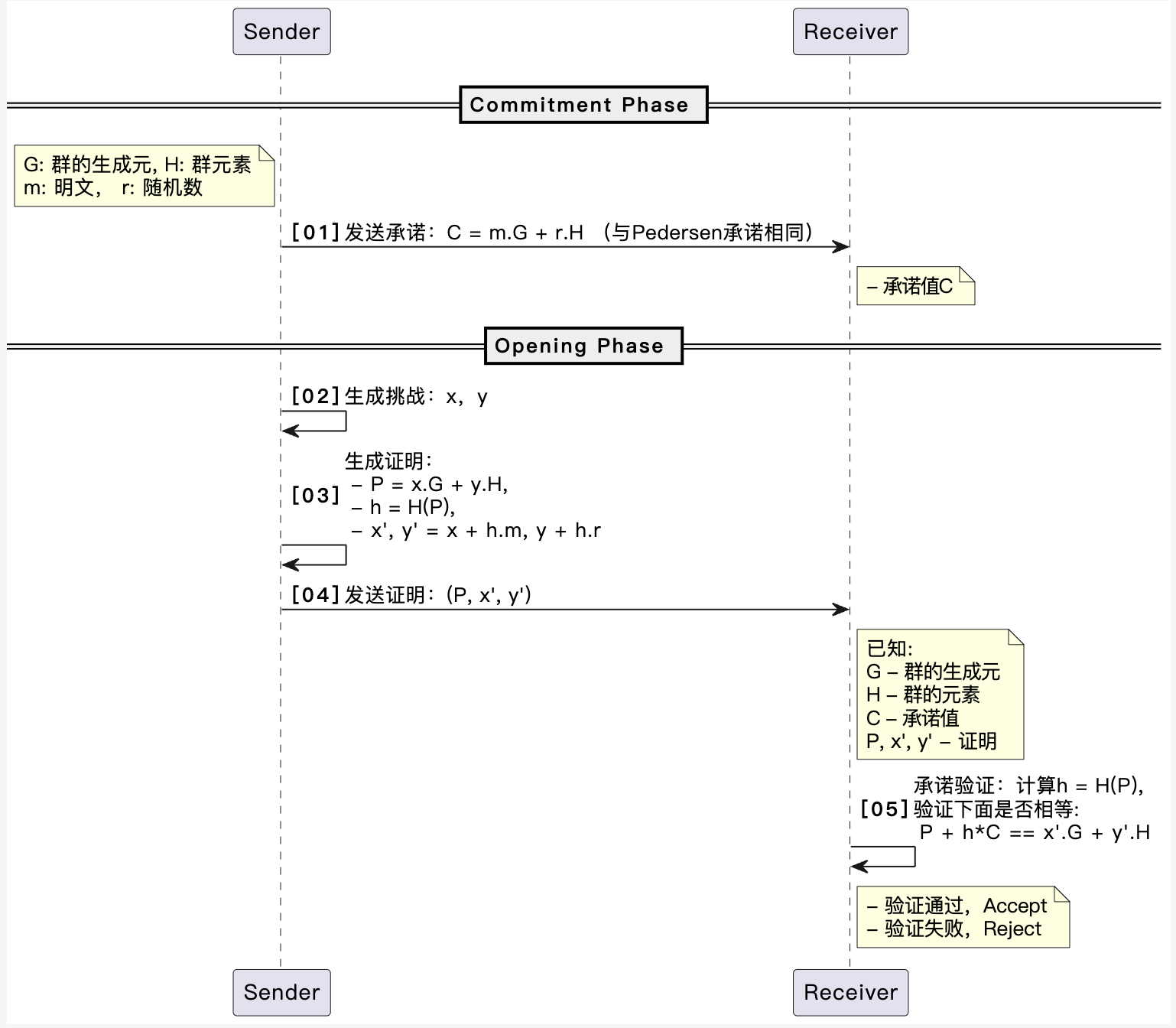
383528-20240923220956953-1454115823.png (1538×1344)

【01】发送承诺：Sender选取随机数 $r$ ，生成承诺 $C=m·G+r·H$

【02】生成挑战：Sender计算两个随机数

【03】生成证明：Sender计算 $P=x·G+y·H$ ，并计算 $h=H(P)$ ，然后计算 $x'=x+h·m$ 和 $y'=y+h·r$

【04】发送证明：Sender发送证明 $(P,x',y')$ 给Receiver

【05】验证：Receiver计算 $h=H(P)$ ，并验证 $P+h·C==x'G+y'H$

正确性：

P+h·C=(x·G+y·H)+h·(m·G+r·H)=x.G+y.H+h·m·G+h·r·H=(x+h·m)

KZG Commitment

目标:验证某个函数在某些特定点上的值是否正确，即在不暴露整个函数细节的基础上，对函数的值进行验证

验证多项式 $f(x)$ 在 $x=i$ 的点上， $f(i)=y$

我们先给定两个椭圆曲线群 $\mathbb{G}_1$ 、 $\mathbb{G}_2$ ，均为循环群，每个椭圆曲线群的阶数 $p$ 相同

取 $G_1$ 、 $G_2$ 分别为 $\mathbb{G}_1$ 、 $\mathbb{G}_2$ 的生成元，我们定义一个双线性映射 $e:\mathbb{G}_1*\mathbb{G}_2\rightarrow\mathbb{G}_T$

可得到:

对任意的 $G_1\in\mathbb{G}_1,G_2\in\mathbb{G}_2$ ，以及标量 $a,b\in\mathbb{Z}_p$ (模 $p$ 的有限域)

都有 $e(aG_1,bG_2)=ab·e(G_1,G_2)$

我们再给定一个 $n$ 次的多项式函数 $f(x):\mathbb{Z}_p\rightarrow\mathbb{Z}_p$ ，另 $a_n\neq0$

f(x)=\sum_{i=0}^{n} a_i x^i=a_0+a_1x+...+a_nx^n

秘密参数 $τ$ 由可信第三方随机生成，给出公开参数 $\tau \cdot G_1,\tau^2 \cdot G_1,\tau^3 \cdot G_1,···,\tau^n \cdot G_1$ 生成后丢弃 $τ$ ， $τ$ 的值发送方和接收方均未知

【01】发送方发送承诺C

发送方选定 $f(x)$ ，发送承诺

C=f(τ)·G_1

我们推导一下:

\begin{aligned} C=[f(τ)]G_1 &=[\sum_{i=0}^{n}a_iτ^i]G_1\\ &=\sum_{i=0}^{n}[a_i]([τ^i]G_1)\\ &=\sum_{i=0}^{n}[a_i][τ^i]G_1 \end{aligned}

由此，因为 $a_i$ 都已知，也有公开参数 $\tau^i\cdot G_1$ ，所有很容易可以在不知道 $τ$ 的情况下计算出 $C$

要想知道 $f(i)=y$ 是否成立，我们可以给定假设，若 $f(i)=y$ 成立，则有在 $x=i$ 时， $f(x)-y=0$

所以由因式定理:对任意的 $i\in\mathbb{Z}_p$ ，都有 $x-i$ 能够整除 $f(x)-f(i)$

构造出辅助多项式 $h_i(x)$ : $h_i(x) = \frac{f(x) - f(i)}{x - i}$ ， $h_i(x)$ 的次数为 $n-1$ ， $x=i$ 为 $h_i(x)$ 的零点

故将 $\pi$ 作为Proof: $\pi=h_i{τ}·G_1$

【02】发送方发送安全参数

\pi=h_i(τ)·G_1

推导如下:

\begin{aligned} \pi&=h_i(τ)·G_{1}\\ &=[\sum_{i=0}^{n-1}\frac{f(τ) - f(i)}{τ - i}]G_1\\ &=\sum_{i=0}^{n-1}\frac{(f(τ)-f(i))·G_1}{G_1^{-1}·{G_1}(τ-i)} \end{aligned}

分子部分同公式(6)处可以计算，分母部分 $G_1^{-1}$ 由 $G_1$ 为 $\mathbb{G}_1$ 的元素可知， $G_1$ 必有逆元； ${G_1}(τ-i)$ 可由公开参数计算。

【03】接收方验证安全参数与承诺

e(\pi,(τ-i)·G_2)=e(C-y·G_1,G_2)

推导如下:

\begin{aligned} &\;\;\;\;\;(\pi,(τ-i)·G_2)\\&=e(h_i(τ)·G_1,(τ-i)G_2)\\&=e(((f(τ)-f(i))·G_1,G_2)\\&=e(C-y·G_1,G_2) \end{aligned}

等式成立则可证在 $x=i$ 处， $f(i)=y$

利用拉格朗日插值法

多项式

构造

I(x)=\sum_{i=0}^{n-1}y_i\prod_{j=0,j \neq i}^{n-1} \frac{x -x_j}{x_i-x_j}

例如当 $n=3$ 时

f(x)=y_0 \frac{(x-x_1)(x-x_2)}{(x_0-x_1)(x_0-x_2)}+y_1\frac{(x-x_0)(x-x_2)}{(x_1-x_0)(x_1-x_2)}+y_2\frac{(x-x_0)(x-x_1)}{(x_2-x_0)(x_2-x_1)}

只有当 $x=x_i$ 时，此时才有 $f(x_i)=1·y_i$

从以上例子来看，可以以此实现批量验证，只需要传递多个 $x$ 的位置信息，就能查询该点的 $f(x)$ 值，而无需透露整个多项式的具体系数

由公式(7)，我们能假设 $x_0,x_1,...,x_{n-1}$ 均为零点

可以给定一个零多项式

Z(x)=(x-x_0)(x-x_1)···(x-x_{n-1})

同上，能有 $f(x)-I(x)$ 能被 $Z(x)$ 整除

我们可以构造出辅助多项式 $q(x)$ : $q(x)=\frac{f(x)-I(x)}{Z(x)}$

那么同样的，可以给定 $proof\;\pi=q(τ)·G_1$

接收方可以使用如下等式进行验证

e(\pi,Z(τ)·G_2)=e(C-I(τ)·G_1,G_2)

向量

定义：对一个长度为q的有序序列 $(m_1,...,m_q)$ 进行承诺，之后在特定位置揭示承诺值

只需要取一个n维向量 $\vec{a}$ ，在 $\vec{a}$ 中， $a_1$ 存储着多项式 $f(x)$ 在 $x=1$ 处的值，本质上是用 $\vec{a}$ 来存储 $f(x)$ 的函数值。

可以列出

f(x)=\sum_{i=1}^{n}a_i·I_{i,n}(x)

其中的 $I_{i,n}(x)$ 为拉格朗日函数，同公式(7)所示，当且仅当 $x=i$ 时， $I_{i,n}(x)=1$ ，其余均为0

具体证明同上

更新承诺

C':=C+(a_i'-a_i)⋅I_{i,n}(τ)⋅G_1

若 $I_{i,n}(τ)·G_1$ 的所有值都已经缓存在服务器中，此时再更新承诺，就只需要在椭圆曲线 $\mathbb{G}_1$ 进行一次乘法和一次加法，时间复杂度为O(1)

特殊方案-引入陷门trapdoor

Trapdoor Commitment

方案目标:确保消息内容保密的同时，允许承诺方灵活处理消息的承诺方案。

符号说明:

$κ$ :保密参数-security parameter
$cpp$ :公开参数-public parameter
$tr$ :陷门参数-trapdoor
$\vartheta$ :随机数-random number
$c$ :公开的承诺字符串-the commitment string
$m$ :消息-message

C.setup( $1^{κ}$ )

输入:安全参数κ
输出:公开参数 $cpp$ 与陷门 $tr$

C.commit( $cpp,m,\vartheta$ )

输入: $cpp,m,\vartheta$
输出:c

$m$ 为消息空间 $\mathcal{M}$ 中的值， $c$ 为承诺空间 $\mathcal{C}$ 中的值，这些都在公开参数 $cpp$ 中

C.equivocal( $cpp,c,(m,\vartheta),m',tr$ )

输入: $cpp,c,m,\vartheta,m',tr$
输出: $\vartheta'$

C.decommit( $cpp,c,m',\vartheta$ )

在这个阶段，发送方会公布消息 $m'$ 、随机数 $\vartheta'$

接收方验证 $c=C.commit(cpp,m',\vartheta')$ ，若成立则 $output(1)$

优点:

1、可以有效抵御重放攻击、选择消息攻击、欺骗攻击以及后向欺骗攻击等

2、利用陷门 $tr$ 将于原本承诺值c关联的消息 $m$ ，更新为与消息 $m'$ 关联，使得能够通过陷门将承诺值 $c$ 与不同的消息进行匹配，相当于给发送方提供了在特殊情况下修改消息的渠道。

总结:

承诺方在拥有陷门 $tr$ 的条件下，可以选择是否修改承诺消息 $m$
而对于 $m$ 是否已经被修改，这个问题不是接收方关心的，接收方只关心在decommit阶段，收到的消息 $m'$ 、随机数 $\vartheta'$ 是否与 $c$ 匹配

RSA方案实现

C.setup( $1^{κ}$ )

cpp取(n,e)，门限tr当作私钥

C.commit( $cpp,m,\vartheta$ )

发送方生成承诺c $c=(m+\vartheta)^e\;mod\;n$

C.equivocal( $cpp,c,(m,\vartheta),m',tr$ )

目标:生成新的随机数 $\vartheta'$ ，使得新承诺 $c'$ 对新消息 $m'$ 是有效的
发送方先解密承诺值 $c$ 有: $m+\vartheta=c^{tr}\;mod\;n$

再生成新随机数 $\vartheta'$ : $\vartheta'=(c^{tr}-m')\;mod\;n$

C.decommit( $cpp,c,m',\vartheta'$ )

接收方计算 $c'$ $c'=(m'+\vartheta')^e\;mod\;n$ 比较 $c=c'$ 是否成立即可验证承诺。